3D Reconstruction
.
To begin, we have the 2D position of each point on the camera. And our goal is to reconstruct the 3D position of this points. To simplify, we suppose that each camera see the point we consider. To do our reconstruction, we need at least two 2D coordinates, i.e. 2 cameras.
Notations:
We use the following notations :
- The 2D position mesured on the camera i is noted (Ui*,Vi*);
- (Ui,Vi) are the projected coordinates of a 3D point on the camera i.
- We note n the number of cameras.
- A 3D point is noted :
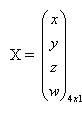
This point is written in homogeneous coordinate, it has also 4 coefficients.
The P matrix :
The matrix P is a transformation matrix from 3D (world locate) to 2D (camera locate). The expression is the following one :
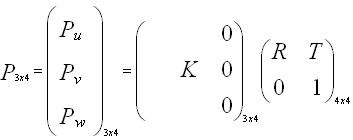
The matrix P is also a matrix exprimated with the parameters sent by MATLAB. The matrix K is the matrix of intrinsic parameters. fu and fv represent the focal distance of the camera, and u0 and v0 the the coordinates of the main point. R is the rotation matrix (3x3) and T the translation vector (3x1).
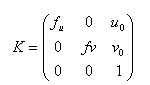
The P matrix of a camera llet us projecting the 3D coordinates on the camera. Indeed, we can compute Ui and Vi :
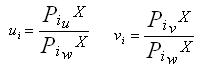
The problem :
To find the 3D place of a point, we want to minimize the distance between each measured position of the point on the camera and its projected position. We sum up to this equation :
.PNG)
Our goal is to minimize it, so we want to solve the equation e(x)=0.
The precedent equation can be reasumed in this system :
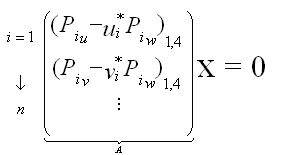
Each Camera has 2 lignes in this equation. The matrix A is also a 2n x 4matrix
Thus, we obtain a system that we can solve using the SVD developped in OpenCV.
The principle of the SVD is t decompose the matrix A in that form :

U and V are two orthogonal matrices, and S is a diagonal one.
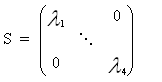
The fonction cvSVD of OpenCV impose us to bring a square matrix.
Thus, if we have only two cameras seeing the point, A is square and we can apply this method.
In the other cases, we use a easy way, which is to multiply A on the left by its transposed matrix.
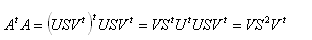
We obtain also a square matrix 4x4, and we can apply the normal method.
cvSVD returns us the matrices S and V. We search for the minimum value of in S.
The diagonal matrix S is made of singular values. Then, we have to search the minimum of these values and to take the corresponding Vi (lign vector) corresponding.(Dim = 4). Thanks to this vector, we have the 3D position X :
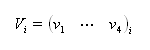
The solution is :

This method is a good one, but the problem is the object we want to reconstruct is not ever seen by all the cameras. We have to set in the matrix A only the cameras that see the object (at least 2 cameras to reconstruct a point...)!
|